Tutoriel Python - sommaire

Mathématiques avec Python

Dans ce chapitre je vais traiter des module statistic & fractions, revenir sur le module math et évoquer la bibliothèque matPlotlib mais auparavant je vais rappeler quelques fonctions natives orientées mathématiques.

Fonctions natives à vocation mathématiques

Commandes à saisir dans la console. >>> notes = [7,10,13,11,9] >>> sum(notes) 50 >>> len(notes) 5 >>> sum(notes)/len(notes) 10.0 >>> max(notes) 13 >>> min(notes) 7 >>> sorted(notes) >>> notes [7, 9, 10, 11, 13]

J'ai pu calculer la moyenne simple de la série : 50/5 = 10 en combinant les fonctions sum() & len().
Je peux dire grâce à la liste triée, que la médiane est 10 (élément du milieu dans la série ordonnée).

Module statistics

Créer une commande qui calcule la moyenne simple d'une série de notes, c'est facile. Par contre la programmation de la variance, de l'écart type c'est beaucoup plus compliqué. Donc ce module tombe à pic car il propose des fonctions de haut niveau ad hoc.

Liste des fonctions du module

Test de certaines fonctions

Pour importer le module statistics j'utilise la syntaxe : import nomModule as alias
Donc pour produire une commande j'utilise la syntaxe : alias.fonction(). L'emploi d'un alias a ici du sens car le nom du module est ici compliqué.

Syntaxes

mean(série) : fonction qui calcule la moyenne simple d'une série de notes.

La médiane est une valeur qui permet de partager une série numérique ordonnée en deux parties de même nombre ; syntaxe : median(série)

le mode désigne la valeur la plus représentée dans une série ; syntaxe : mode(série)

L’écart type est un indicateur de dispersion dans une série ; syntaxe : stdev(série)

Vous constatez ici, que pour les deux séries la moyenne est pratiquement la même (12,2 et 12,0).
Mais le premier élève est beaucoup plus irrégulier dans ses résultats que le second. Donc l'écart type est plus grand pour le premier que pour le second.
Je rappelle que l'écart type est la racine carrée de la variance. Il existe bien sûr la fonction variance() dans le module statistics.

Pour les mordus de statistiques, le module propose aussi des fonctions pour calculer les moyennes géométrique & harmonique ...

Le module fractions

Vous pouvez manipuler des fractions sous Python grâce au module fractions.
Un seul exemple, il est plus logique d'utiliser la fraction "1/3" que le flottant correspondant qui n'est qu'une valeur approchée de ce nombre irrationnel.

Quelques commandes à tester

Le module fractions comprend surtout la fonction Fraction (avec un F majuscule).

Commentons les commandes ci-dessus :
• importation du module
• la fonction Fraction est argumentée par deux entiers (numérateur, dénominateur) ou par une chaîne ("numérateur/dénominateur")
• on peut additionner, soustraire, multiplier, diviser plusieurs fractions ; Python réduit au même dnominateur si nécessaire :
  - addition : 1/3 + 1/2 = 5/6 ou dans le jargon Python : Fraction(5,6)
  - soustraction : 1/2 - 1/3 = 1/6 ou en Python : Fraction(1,6)
  - mu1tiplication : 1/4 * 1/3 = 1/12 ou en Python : Fraction(1,12)
  - division : 1/3 / 1/4 = 4/3 ou en Python : Fraction(4,3). Donc il a bien effectué 1/3 * 4/1
• float(unTiers+unQuart) : on peut convertir une fraction en flottant avec la fonction float() ; 1/3 + 1/4 = 7/12 soit environ 0.5833333 ...
• Fraction(6/12) retourne Fraction(1,2) : donc la fraction est simplifiée

Utiliser une fraction plutôt qu'un flottant

Il y avait dans le passé un taux de TVA dit majoré qui était égal à 1/3 du hors taxes. Il s'appliquait entre autres au matériel HIFI et aux voitures neuves.
Voyons comment il fallait alors calculer la TVA par rapport au prix hors taxes de l'article. >>> taux_tva = Fraction(1/3) >>> hors_taxe = 1000 >>> TVA = round(float(hors_taxe * taux_tva),2) >>> TVA 333.33

La TVA sur l'article qui vaut 1000 HT est calculé en appliquant le taux sous forme d'une fraction.
Dans la même commande le résultat est arrondi à deux décimales. J'ai donc imbriqué les fonctions round & float.

Module math

Dans un chapitre précédent ce module a simplement été évoqué. Je vais maintenant approfondir.

Une liste impressionnante de fonctions

Testons avec la console interactive certaines de ces fonctions.
Qui doivent être ici préfixées, compte tenu de la syntaxe utilisée pour l'importation du module. Mais nous avons bien fait car si nous avions écrit from math import * nous aurions écrasé la fonction native pow(). Il existe en effet une fonction math.pow(). >>> math.ceil(3.5) 4 >>> math.floor(3.5) 3 >>> math.fabs(-10) 10.0 >>> math.factorial(5) 120 >>> math.remainder(10,3) 1.0 >>> maliste = [10,15,12,18] >>> math.fsum(maliste) 55.0 >>> monset = {10,15,12,9} >>> math.fsum(monset) 46.0 >>> montuple = (10,12,14) >>> math.fsum(montuple) 36.0 >>> math.gcd(60,90) 30 >>> math.hypot(4,3) 5.0 >>> math.modf(17.25) (0.25, 17.0) >>> round(3.99) 4 >>> math.pi 3.141592653589793 >>> pow(10,5) 100000 >>> math.pow(10,5) 100000.0 >>> math.fmod(10,3) 1.0

Les fonctions testées ci-dessus :
• ceil(nombre) : arrondit à l'entier supérieur
• floor(nombre) : arrondit à l'entier inférieur
• fabs(nombre) : retourne la valeur absolue
• factorial(n) : retourne la factorielle de l'entier n : 1*2 ... * n
• remainder(dividende, diviseur) : retourne le reste de la division entière ; équivaut à l'expression : dividende%diviseur
• fsum(liste) : retourne la somme des éléments d'une liste, tuple ou ensemble(set)
• gcd(n1,n2): retourne le plus grand commun diviseur entre plusieurs entiers
• hypot(4,3): donne la valeur de l'hypothénuse à partir des côtés de l'angle droit ; équivaut à math.sqrt(4** + 3**)
• modf(flottant): décompose un nombre décimal en partie entière et partie décimale sous forme d'un tuple
• pi : pi n'est pas une fonction du module mais une constante. Donc pas de parenthèses après "pi"
• Il y a deux fonctions pow() : la fonction native et la fonction dans le module math ; la fonction native retourne un entier alors que la fonction du module retourne un flottant
• fmod() : retourne le reste de la division euclidienne

Concernant l'objet factorial(), rappelez vous, dans un chapitre précédent nous nous sommes fatigués à produire (de deux façons) une fonction retournant la factorielle d'un nombre. Donc nous avons travaillé pour rien ? Pas vraiment, car nous avons ainsi découvert à cette occasion une notion importante en algorithmique : la récursivité.

Trigonométrie

Le module math comprend également toutes les fonctions relatives à la trigonomètrie :

• des fonctions pour convertir radians en degrés ou vice versa
• des fonctions pour calculer sinus, cosinus, tangente à partir d'un angle en radians
• des fonctions pour calculer angles en radians à partir de sinus, cosinus ou tangente.

Rappels : unité d'angle radian

Le radian est une unité de mesure pour mesurer les angles. Un angle d'un radian est un angle qui délimite un arc de cercle d'une longueur égale au rayon du cercle.
Ci-dessous un gif animé qui explique bien la notion de radian :
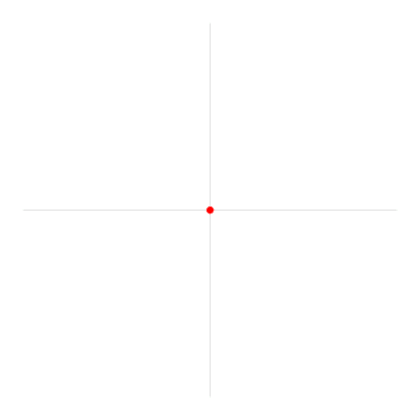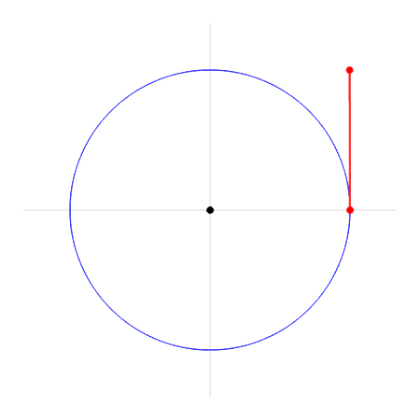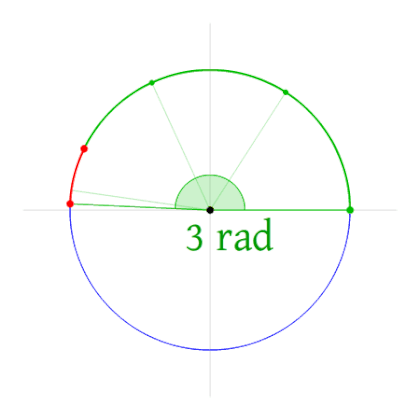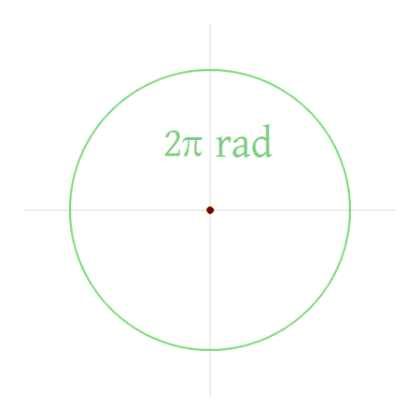
Un cercle complet (360°) représente un angle de 2π radians. Donc un angle plat c'est π radian et un angle droit c'est π/2 radian.

Rappels de trigonométrie

La trigonométrie est une branche des mathématiques qui traite des relations entre distances et angles dans un triangle rectangle. Sinus, cosinus et tangente sont des rapports entre deux côtés du triangle rectangle. Mais à partir du sinus (ou cosinus ou tangente) on peut déterminer l'angle correspondant.

Quelques fonctions trigonométriques proposées par le module math

Vérifions tout cela dans l'interpréteur : >>> import math >>> math.pi 3.141592653589793 >>> math.radians(360) 6.283185307179586 >>> math.degrees(2 * math.pi) 360.0 >>> math.sin(radians(45)) 0.7071067811865476 >>> math.sin(radians(60)) 0.8660254037844386 >>> math.sin(radians(30)) 0.49999999999999994

math.pi retourne 3.1416... environ.
L'équivalent de 360° en radians est 6,28 radians.
L'équivalent de 2 ∏ radians = 360°
La fonction radians(angle en degrés) convertit les degrés en radians.
La fonction degrees(angle en radians) convertit les radians en degrés.
La fonction sin(angle en radians) retourne la valeur du sinus. Donc si vous voulez partir d'un angle en degrés il faut imbriquer la fonction radians(angle en degrés) dans sin()
Il existe aussi les fonctions : cos(), tan()

Rappels sur le calcul du sinus, cosinus et tangente d'un angle

Après avoir calculé le sinus ou cosinus ou tangente d'un angle, il fallait rechercher ensuite dans les tables trigonométriques l'angle correspondant.
J'emploie le passé car désormais la recherche d'une valeur d'angle se fait avec une calculette scientifique OU avec Python.

Exercice de trigo

Un triangle rectangle a des côtés de l'angle droit qui mesurent respectivement 3 et 4.
Calculez l’hypoténuse, et les deux angles (autres que l'angle droit) en degrés.

Résolvons ce problème via l'interpréteur Python >>> from math import * # avec cette syntaxe, il est inutile de préfixer les fonctions du module math >>> a=4 >>> b=3 >>> h =sqrt(pow(a,2) + pow(b,2)) #j'aurais pu utiliser la fonction hypot >>> h 5.0 >>> h =math.hypot(a,b) >>> h 5.0 >>> angle1 = degrees(asin(b/h)) >>> angle 36.86989764584402 >>> angle2 = degrees(asin(a/h)) >>> angle2 53.13010235415599 >>> >>> angle1 + angle2 90.0

Avec la commande from math import * je ne serai pas obligé de préfixer les fonctions du module math dans les commandes qui suivent.

Le carré de l’hypothénuse est égal à la somme des carrés des côtés de l'angle droit.
Donc l'hypothénuse est ici égale à 5
Donc le sinus du premier angle = 3/5 soit un angle de 36,87°
Et le sinus du deuxième angle = 4/5 soit un angle de 53,13°
Contrôle : la somme des deux angles est bien égale à 90°

La fonction asin(sinus) donne l'angle en radians à partir de la valeur du sinus ; il faut ensuite le convertir en degrés avec la fonction degrees()
Il existe aussi les fonctions acos(), atan() qui donnent respectivement l'angle en radians à partir du cosinus ou tangente.

Voyez que souvent on est obligé d'imbriquer dans une commande deux fonctions.

La bibliothèque matplotlib

Grâce à cet outil vous allez pouvoir représenter graphiquement des fonctions mathématiques telles f(x) = ax + b(fonction affine) ou des paraboles (f(x) = a x²) voire des hyperboles (f(x) = 1/x), etc.

Matplotlib est donc une bibliothèque pour le traçage de courbes. J'ai bien écrit "bibliothèque" (et non pas module). Donc pour disposer des modules de ce pack il faut éventuellement installer cette extension de Python avec l'utilitaire pip

Tracer des courbes

L'installation éventuelle (avec l'utilitaire pip) d'une extension de Python sera évoquée dans le chapitre 16. Dons pour le moment, supposons que le pack est installé.
Si l'extension est installée il suffit d'importer le module pyplot de cette extension.

Premier tracé

Commandes à tester dans l'interpréteur : >>> from matplotlib import pyplot >>> pyplot.plot([-3,0,3], [-6,0,6]) >>> pyplot.show()

Nous devons importer le module pyplot du package matplotlib.
La fonction plot() permet de définir les couples de points et demande en arguments deux séries de valeurs : la série des abscisses et la série des ordonnées. Ces deux arguments peuvent être des variables qui contiennent des séries de type "range" ou "list".
La fonction show() permet d'afficher le graphique.
Après la dernière commande pyp.show() une fenêtre légendée "figure1" et contenant le graphique s'affiche.

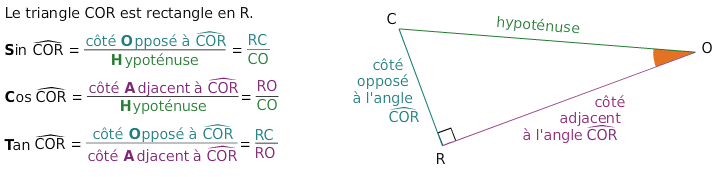
Le graphique :

Il s'agit d'une droite puisque les couples (x,y) correspondent à la fonction y = 2x (une fonction linéaire)
La fonction show() est utilisée sans arguments et est bloquante ; tant que la fenêtre n'a pas été fermée, la suite du code ne s'éxécute pas.

Deuxième tracé

Pour le premier tracé nous n'avions que trois couples (x,y) mais c'était suffisant, puisqu'il s'agissait d'une fonction linéaire.
Pour tracer, par exemple, une parabole il faut beaucoup plus de points ; nous allons donc utiliser toute la puissance de la fonction range(start,stop,step) pour produire un grand nombre de couples.

Commandes à saisir dans l'interpréteur: >>> import matplotlib.pyplot as plt >>>plt.grid() >>>seriex = range(-50,52,2) #série des x >>>seriey= [x**2 for x in range(-50,52,2)] #série des y >>>plt.plot(seriex,seriey) >>>plt.show()

Notez une autre syntaxe pour importer le module pyplot de matplotlib (nomLibrairie.nomModule). Il est d'usage de donner l'alias "plt" à ce module.
plt.grid() : on rajoute une grille dans le repère orthogonal.
Les couples x,y sont créées grâce à la fonction range(start,stop,step).

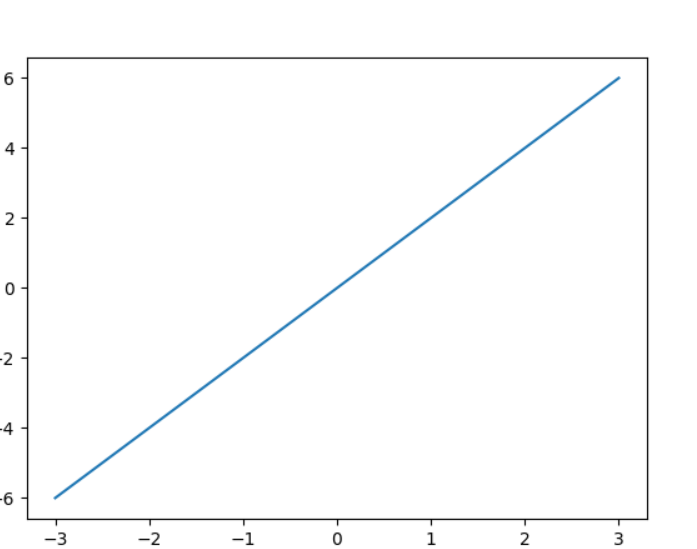
Une superbe parabole apparait dans la fenêtre "figure1".

Il est possible d'enregistrer le graphique au format PNG en cliquant sur la commande "enregistrer" de la fenêtre graphique.

Programmes construisant des graphiques

Pour sauvegarder nos commandes nous allons les stocker dans des programmes.

Réalisation d'un histogramme

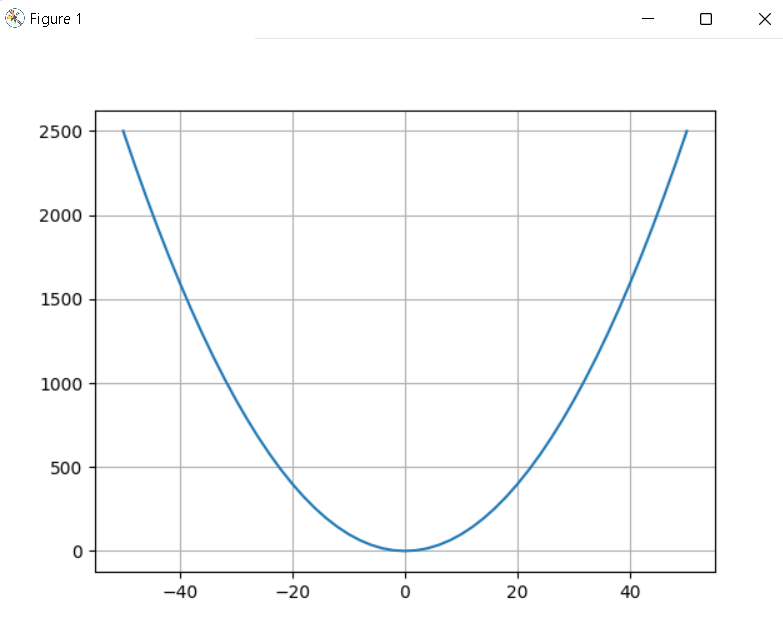
Les histogrammes sont utilisés pour représenter des séries statistiques.
Thème : distribution des notes à un partiel dans un groupe de travaux dirigés.
Le code : # nom programme : graphique1.py # objet : histogramme sur distribution notes dans une classe import matplotlib.pyplot as plt plt.grid() x = [6,8,10,12,14,16] y = [3,5,6,8,7,2] largeur = 0.5 plt.bar(x, y, largeur) plt.show() plt.close()

Le programme demande l'affichage d'une grille dans le repère orthogonal.
x contient la liste des abscisses (notes possibles)
y contient la liste des ordonnées (effectif de chaque note)
Pour produire un histogramme, il faut utiliser la fonction bar(série des x, série des y, largeur de chaque barre)

Le graphique :

Réalisation d'un "camembert"

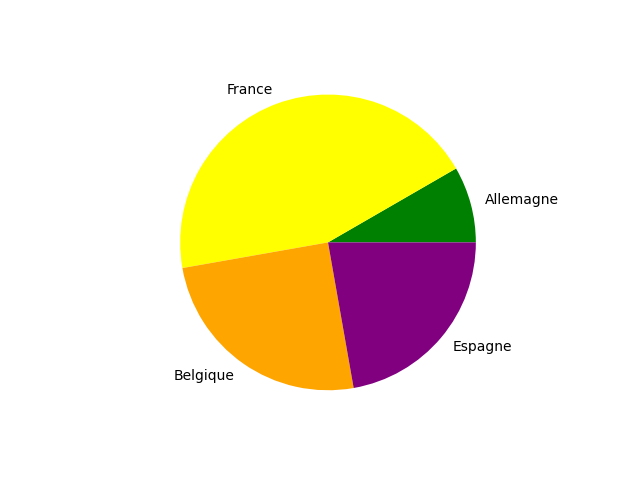
Il faut utiliser la fonction pie(série de valeurs, légendes, couleurs) # nom programme : graphique4.py # objet : camember import matplotlib.pyplot as plt legendes = 'Allemagne', 'France', 'Belgique', 'Espagne' serie = [15, 80, 45, 40] couleurs = ['green', 'yellow', 'orange', 'purple'] plt.pie(serie, labels=legendes, colors=couleurs) plt.show()

Le graphique :

Construction d'un nuage de points

Le code : # nom programme : graphique3.py # objet : nuage de points from matplotlib import pyplot pyplot.grid() x = [1, 2, 3, 4, 5, 6] y = [2, 3.5 ,5.5 ,8.5 ,9.5, 11.5] pyplot.scatter(x, y) pyplot.show() pyplot.close()

Pour produire un nuage de points il faut utiliser la fonction scatter(abscisses, ordonnées)
Le graphique :

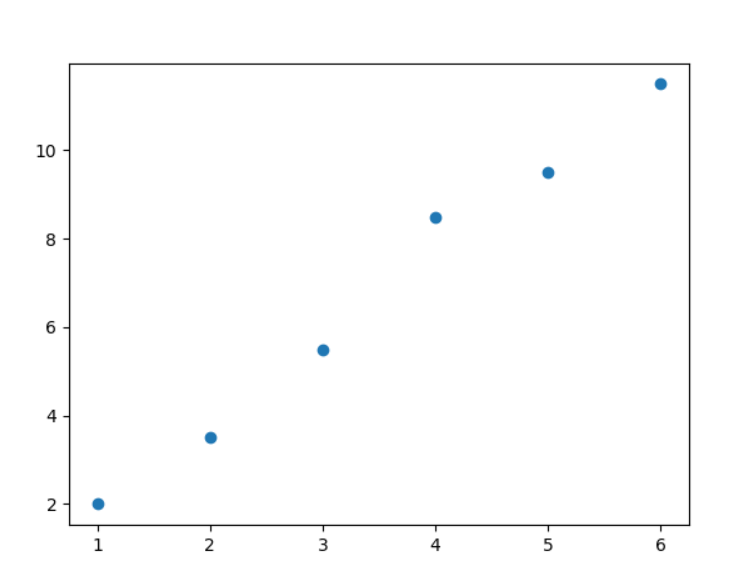
On note une corrélation linéaire presque parfaite : les points sont pratiquement alignés sur une droite.
On ne pourrait pas construire la droite de régression exprimant la relation entre les x et les y ???

Pour approfondir

Un tuto très complet sur le module pyplot de la libraire matplotlib

Récupérer les programmes de ce chapitre

Le fichier ZIP correspondant