Traduction
Tutoriel Python - sommaire
Tutoriel Python - recherche
L'auteur : Patrick Darcheville
 Vous pouvez me contacter via Facebook pour questions & suggestions :
Page Facebook relative à mon site
Vous pouvez me contacter via Facebook pour questions & suggestions :
Page Facebook relative à mon site
 Vous pouvez me contacter via Facebook pour questions & suggestions :
Page Facebook relative à mon site
Vous pouvez me contacter via Facebook pour questions & suggestions :
Page Facebook relative à mon site
 Python propose un module dénommé "turtle" qui permet de dessiner des figures géométriques dans une fenêtre.
Python propose un module dénommé "turtle" qui permet de dessiner des figures géométriques dans une fenêtre.
Ces dessins peuvent être sauvegardés sous forme d'images PNG.
Mais avant d'aborder ce module nous allons faire une petite digression : personnaliser l'IDLE (interface de développement).
Si vous êtes comme moi, vous trouvez que la taille de police dans l'éditeur est trop petite.
Ce n'est pas compliqué d'agrandir la taille de police, le type de police , etc.
Commande : Options / Configurer IDLE
Exemple : cliquez sur l'onglet "Fonts/Tabs" , déroulez la liste "size" et sélectionnez 12
Vous pouvez aussi cliquer sur l'onglet "highlights" (coloration) pour changer la couleur de texte des commentaires.
Vous trouverez le script correspondant en fin de chapitre.
Turtle signifie en anglais "tortue".
C'est avec ce module que l'on peut réaliser dans Python de jolies figures géométriques.
Le principe est simple : on dessine en déplaçant un crayon (ou "turtle" ou tortue ou curseur).
Dans ce chapitre j'emploirai le plus souvent le terme "curseur".
Ce curseur a la forme d'une pointe de flèche.
Créez un nouveau dossier à la racine de C: et nommez le "python_turtle". Tous les scripts de ce chapitre seront stockés dans ce répertoire.
Turtle met en place un repère à deux dimensions dans la fenêtre de dessin. Attention ce repère est invisible.
Les axes X & Y (invisibles) coupent hauteur et largeur de la fenêtre en leur milieu.
Donc l'origine du repère est donc le centre de la fenêtre graphique.
Le curseur est au départ situé au point(0,0) du repère et apparait sous forme d'une flèche orientée vers la droite. Ce qui signifie que tout déplacement avant du crayon se fera vers la droite.
#nom prog. : tortue_exemple.py from turtle import * speed(1) forward(200) left(90) forward(100) right(90) forward(100) left(90) forward(100) left(90) forward(300) mainloop()
Il faut bien sûr importer le module turtle.
La fenêtre graphique a une taille de 950 par 800 pixels par défaut.
Il faut préciser la vitesse de traçage avec la fonction speed(). Ici vitesse très lente car le paramètre vaut 1.
Ensuite vous retrouvez toujours les mêmes types de commandes : forward(pas), left(angle) , right(angle).
Les fonctions forward() & backward() sont argumentées par un entier ; l'unité (le pixel) est implicite.
Les fonctions left() & right() sont arguméntées avec un entier ; l'unité (le degré) est implicite.
Ne pas oubliez de terminer le programme avec l'instruction mainloop() pour redonner la "main à l'utilisateur".
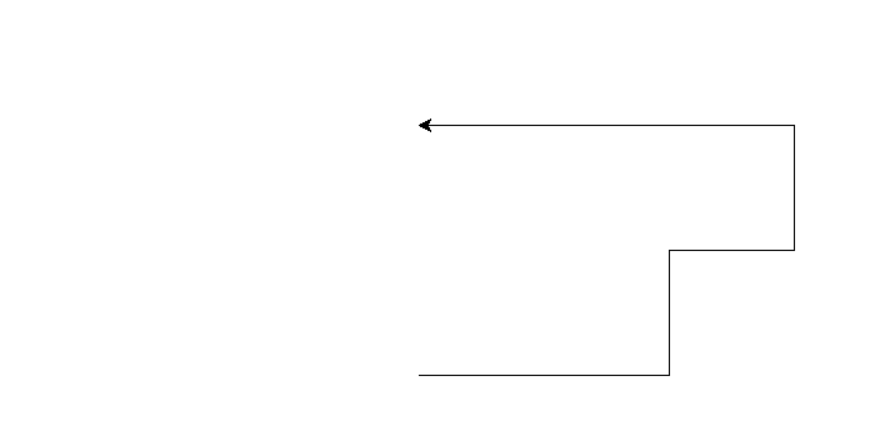
Première chose : le graphique ne s'affiche pas dans la fenêtre "Shell" comme pour un script ordinaire, mais dans une fenêtre graphique : "Python turtle graphics".
Un carré est un polygone régulier de 4 côtés égaux et 4 angles égaux (angles droits).
#nom programme : tortue_carre.py
#objet : dessiner un carre
from turtle import *
speed(1)
pencolor('red')
c =input('côté du carré ? : ')
c=eval(c)
#convertir en numérique la saisie
forward(c)
left(90)
forward(c)
left(90)
forward(c)
left(90)
forward(c)
exitonclick()
Par défaut la couleur du trait est noir. Ici je demande qu'il soit rouge avec la fonction pencolor().
Le côté du carré est saisi dans la variable c.
Rappel : toute saisie avec la fonction input() est de type string ;
il faut donc convertir le contenu de c en un numérique avec la fonction eval().
Ensuite vous avez 4 fois le même couple d'instructions : forward(c) et left(90)
On aurait pu écrire le code d'une façon beaucoup plus correcte sur le plan algorithmique.
... for i in range(5) : #pour i allant de 0 à 4 forward(c) left(90)
# nom programme : tortue_carre_bis.py
from turtle import *
pencolor('purple')
speed(5)
for i in range(50):
forward(20 + (i*10) )
left(90)
mainloop()
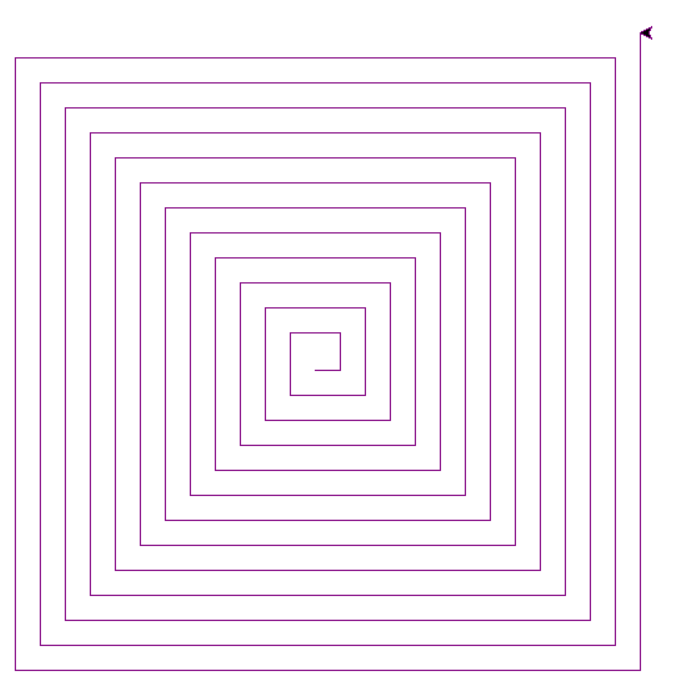
A chaque passage dans la boucle l'argument de la commande forward est plus grand de 10, donc on dessine une sorte de labyrinthe.
Le rendu :
Je veux réaliser un programme très généraliste capable de produire n'importe quel polygone régulier : carré, pentagone, hexagone, octogone.
Dans tous les cas la somme des "virages à gauche" doit être égale à 360° afin que la tortue revienne à sa position de départ.
Donc pour un carré, chaque "virage à gauche" doit avoir un angle de : 360/4 = 90°
Et pour un pentagone , chaque "virage à gauche" doit avoir un angle de : 360/5 = 72°
Et pour un hexagone, chaque "virage à gauche" doit être de : 360° / 6 = 60°
Et 45° pour un octogone.
#nom prog. : tortue_polygone.py
#objet : dessiner un polygone régulier de n côtés (4 ou 5 ou 6 ou 8)
from turtle import *
n ="2"
while n not in "4568": #controle de saisie
n = input ("nombre de côtés du polygone : 4/5/6/8: ")
cote = input("longueur du côté : " )
n =eval(n) #convertir n en numérique
c=eval(cote)
angle=360 / n
for i in range(n):
forward(c)
left(angle)
exitonclick()
Il y a un contrôle de saisie basé sur l'opérateur "not in … " : tant que n n'est pas inclus dans la chaine "4568"
il est possible de répéter la saisie.
Pour qu'il y ait au moins un passage dans la boucle, il faut une valeur initiale à n ne soit pas incluse dans la chaine "4568".
Le programme est très court grâce à une structure "for i in range(n):".
À la place de mainloop() on peut utiliser la fonction exitonclick() ; si clic sur le graphique, l'utilisateur reprend la main.
Le rendu :

Ici j'avais tapé 6 pour obtenir un hexagone.
Je suis d'accord avec vous le dessin est triste : pas de couleur de fond ni de remplissage du polygone.
Un peu de patience ...
Il faut utiliser la fonction cercle(rayon, [angle]).
Le seul argument obligatoire est le rayon.
# nom programme : tortue_cercles.py
import turtle as tu
tu.pencolor('orange')
tu.speed("slow")
for i in range(20):
tu.circle(i +30)
tu.exitonclick()
En raison de la technique d'importation du module, je dois préfixer les fonctions avec l'alias utilisé lors de cette importation.
L'argument de la fonction speed() peut être un entier (entre 0 et 10) mais aussi une chaine : "fast", "normal", "slow", …
Remarque : la tortue tourne à gauche. Si vous voulez qu'elle tourne à droite la valeur du rayon doit être négative.

Je dessine des cercles donc la fonction circle() n'a qu'un argument : le rayon !
Dessiner 15 ronds de la gauche vers la droite.
# nom programme : tortue_cercles_bis.py
import turtle as tu
tu.setup(500,500)
tu.pencolor('orange')
tu.pensize(5)
tu.speed(5)
tu.up()
tu.backward(250)
tu.down()
for i in range(15):
tu.circle(-30)
tu.forward(30)
tu.exitonclick()
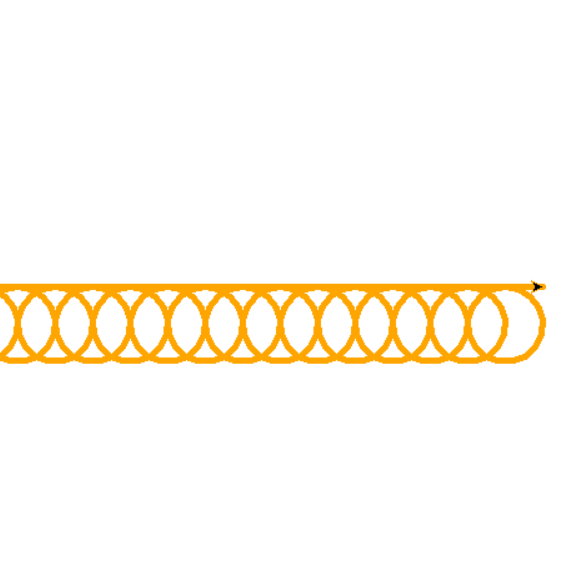
Comment éviter le trait entre chaque cercle ?
Il faut dessiner un rectangle avec aux deux extrémités des demi-cercles.
Le trait doit être très très épais et couleur de l'asphalte.
from turtle import *
# tortue_circuit.py)
setup(800,800)
title("circuit automobile")
bgcolor('lime')
speed('slow')
pencolor('gray')
pensize(50)
up()
right(90)
forward(100)
left(90)
down()
forward(250)
circle(100,180)
forward(500)
circle(100,180)
forward(250)
mainloop()
title("circuit automobile") : je personnalise le titre de la fenêtre graphique.
bgcolor('lime') : la fenêtre a une couleur de fond
La fonction circle() a ici deux arguments : rayon (en px) & angle (exprimé en degrés)
On voit ici les limites des fonctions forward(), left(), right(), etc.
Il faut 3 instructions (right(90), forward(100), left(90)) pour déplacer le curseur vers le bas de 100px.
On aurait pu remplacer tout simplement par l'instruction unique goto(0,-100). Voir plus loin dans ce
chapitre.

Vous pouvez souhaitez que la forme dessinée soit remplie d'une certaine couleur.
Reprenons le programme "tortue_polygone.py" et améliorons le !
#nom prog. : tortue_polygone_plus.py
#objet : dessiner un polygone régulier de n côtés (4 ou 6 ou 8 ou 10)
from turtle import *
setup(600,600)
speed('slow')
pencolor('purple')
pensize(5)
fillcolor('lime')
bgcolor('pink')
n ="2"
while n not in "4568": #controle de saisie
n = input ("nombre de côtés du polygone : 4/5/6/8 : ")
cote = input("longueur du côté : " )
n =eval(n) #convertir n en numérique
c=eval(cote)
angle=360 / n
begin_fill()
for i in range(n):
forward(c)
left(angle)
end_fill()
exitonclick()
Le graphique obtenu après avoir saisi 5 et 200 :

# nom programme : tortue_infos py
from turtle import *
hideturtle()
for i in range(4): #boucle effectuée 4 fois (0 à 3)
print ("position tortue : ", position())
forward(200)
left(90)
# fin boucle
print("-----")
up()
home()
print ("position tortue : ", position())
mainloop()
La fonction position() retourne les coordonnées x et y de la tortue à un stade donné.
La fonction home() déplace le curseur à l'origine du repère (x = 0 ; y = 0).
La fonction hideturtle() masque le curseur
position tortue : (0.00,0.00) position tortue : (200.00,0.00) position tortue : (200.00,200.00) position tortue : (0.00,200.00) ----- position tortue : (0.00,0.00)
En parenthèse la valeur de l'abscisse puis celle de l'ordonnée de chaque angle.
Un carré est dessiné. Le curseur ("turtle") n'apparait pas car il est masqué.
Il existe aussi la fonction showturtle() pour réafficher le curseur.
Rappel : un triangle équilatéral est un triangle dont les 3 côtés et les trois angles sont égaux.
Comme la somme des angles d'un triangle est toujours égale à 180°, chaque angle d'un équatéral fait 180/3 = 60°
#nom programme : equilateral.py
from turtle import *
setup(600,600)
speed('slow')
pencolor('red')
fillcolor('lime')
pensize(3)
begin_fill()
forward(200)
left(120)
forward(200)
left(120)
forward(200)
end_fill()
exitonclick()
Chaque angle doit faire 60° et pourtant je programme des "left(120)" ...
L'explication est simple : pour former un angle interne de 60° il faut faire effectuer à la tortue un virage très
serré de (180° - 60° = 120°).
C'est la notion d'angles supplémentaires (somme de deux angles supplémentaires = 180°).
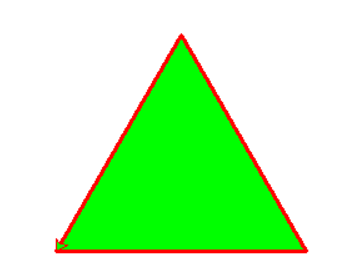
Pour masquer le curseur, rajoutez la commande hideturtle()
En fait une étoile à 6 branches ("étoile de David") est faite de deux triangles équilatéraux qui se superposent.

Il faut donc dessiner le premier triangle équilatéral puis lever le "crayon", déplacer la tortue vers le point (0,100) et dessiner le deuxième triangle.
... #fin premier triangle up() home() goto(0,100) down() #début deuxième triangle right(60) ...
Suite au premier triangle, le curseur était dirigé vers la gauche et vers le bas. Il faut qu'il soit de nouveau disposé à tracer vers la droite grâce à l'instruction home() !
La fonction goto(x,y) sera expliquée plus loin.
Plutôt que d'utiliser les fonctions forward(), backward() left(), right() nous allons utiliser la fonction goto(x,y). qui est beaucoup plus intiutive pour un mordu de math.
Pour utiliser la fonction goto() il faut bien avoir en tête qu'un repèren cartésien (mais masqué) divise la fenêtre
en 4 zones comme le rappelle le croquis ci-dessous :
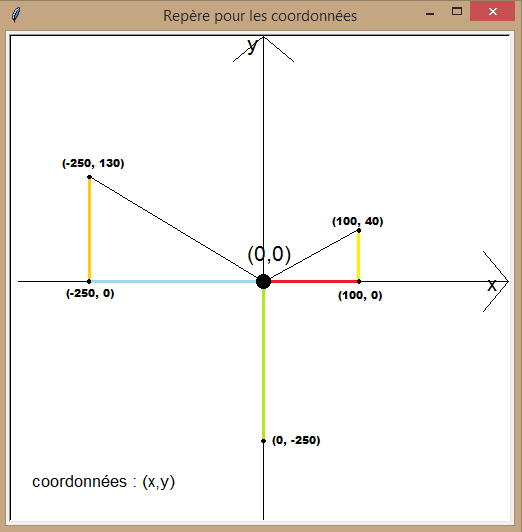
Un point situé à gauche de l'axe des Y et sous l'axe des X a des coordonnées négatives !
# nom programme : tortue_goto.py
from turtle import *
speed('slow')
up()
goto(-300,-300)
down()
goto(300,-300)
goto(300,300)
goto(-300,300)
up()
goto(-100,-100)
down()
goto(100,-100)
goto(100,100)
goto(-100,100)
goto(-100,-100)
up()
goto(0,0)
down()
write ("hello !", font=("Arial", 14, "normal"))
mainloop()
Remarques :
goto(0,0) équivant à home()
La fonction write() permet d'écrire du texte dans la fenêtre graphique.

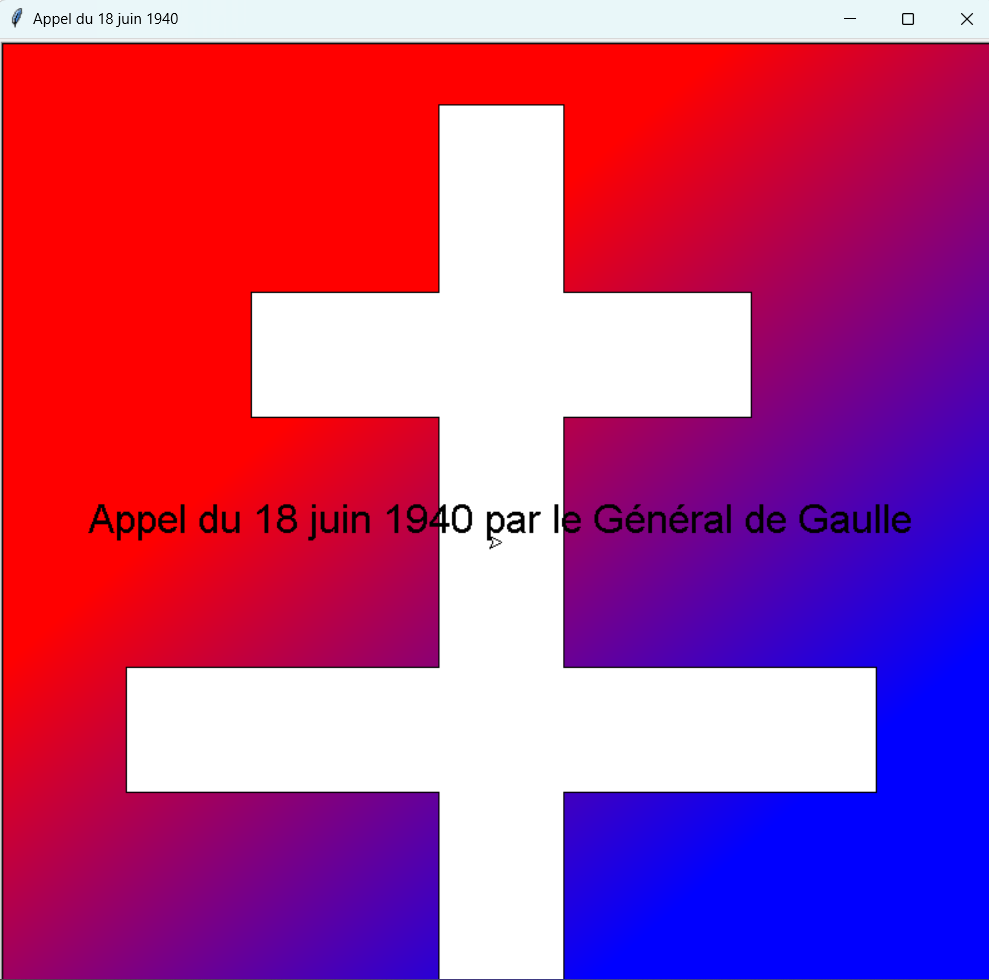
En début de chapitre je vous ai présenté une croix de Lorraine avec en fond un dégradé.
Je vous explique maintenant comment réaliser cette image PNG avec Turle.
from turtle import *
# tortue_appel_18_juin.py
setup(800,800)
hideturtle()
title("Appel du 18 juin 1940")
bgpic("degrade.png")
fillcolor('white')
speed('slow')
pensize(1)
up()
goto(50,350)
begin_fill()
down()
goto(-50,350)
goto(-50,200)
goto(-200,200)
goto(-200,100)
goto(-50,100)
goto(-50,-100)
goto(-300,-100)
goto(-300,-200)
goto(-50,-200)
goto(-50,-350)
goto(50,-350)
goto(50,-200)
goto(300,-200)
goto(300,-100)
goto(50,-100)
goto(50,100)
goto(200,100)
goto(200,200)
goto(50,200)
goto(50,350)
end_fill()
up()
home()
down()
write ("Appel du 18 juin 1940 par le Général de Gaulle", align ="center", \
font=("Arial", 24, "normal"))
mainloop()
J'ai utilisé la fonction bgpic(chemin image) pour insérer l'image en fond de fenêtre.
L'image "degrade.png" a été produite avec le logiciel Inkscape. Il s'agit d'un dégradé rouge vers bleu. Puis le document
Inkscape a été exporté au format PNG.
Avant d'encoder j'ai dessiné la croix de Lorraine sur une feuille de papier à petits carreaux à raison d'un cm pour 100px.
Le croquis me donnant donc les coordonnées x,y de chaque point, le paramétrage des fonctions goto() devient alors un jeu
d'enfant.
Pour en savoir plus sur le module turtle :
>>> import turtle >>> dir(turtle) ...
Le nombre de fonctions du module est impressionnant !
Attention si vous voulez tracer des droites et courbes correspondant à des fonctions du 1er et deuxième degrés, il faut
utiliser un autre module : matplolib.
Python et les mathématiques